Honda gravitatoria (I)

En los comentarios del envío anterior, se ha mencionado varias veces una maniobra utilizada por las sondas interplanetarias actuales, para ahorrar combustible. Se trata de la llamada asistencia gravitatoria, aunque se la conoce más coloquialmente con el nombre de "honda gravitatoria". Alguna vez habremos oído o leído noticias en las que se dice que determinada sonda se dirige hacia determinado planeta, para adquirir más velocidad, aprovechando su gravedad. Uno de los ejemplos más recientes y conocidos es la sonda Cassini/Huygens, con destino Saturno. En vez de ser lanzada directamente hacia su objetivo, se dirigió primero hacia Venus, con el que utilizó esta maniobra dos veces, después volvió hacia la Tierra, para repetir esta maniobra, y finalmente utilizó a Júpiter de la misma manera, antes de dirigirse definitivamente hacia Saturno (la web de la ESA, tiene una bonita animación).

Pero leyendo en envío anterior, o recordando las lecciones de física del cole, uno se pregunta ¿cómo es posible? En efecto, si nos situamos en el planeta utilizado como honda gravitatoria, veremos que si medimos la velocidad de la sonda y su distancia a nosotros, la relación entre ambas será la misma al acercarse y al alejarse. Es decir, salvo el inevitable cambio de dirección, no parece que esta maniobra modifique la velocidad. Si a D km de distancia, la sonda se acercaba a V km/h, una vez completada la maniobra y alejarse otra vez D km, la sonda viajará a esos mismos V km/h.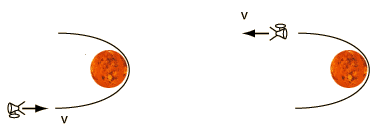

¿Entonces? Bueno, veamos que ocurre si en vez del "planeta honda", utilizamos como sistema de referencia la estrella que orbita. Es decir, en el caso de nuestro sistema planetario, utilizamos nuestro Sol. El planeta se mueve a determinada velocidad, a la que llamaremos U. A una distancia D del planeta, la sonda tenía una velocidad V con respecto a éste. Pero en nuestro nuevo sistema de referencia, al moverse también el planeta, la sonda tendrá una velocidad V+U con respecto a nosotros.

Aquí hay que detenerse un momento a recordar que la velocidad es una magnitud vectorial. Es decir, tiene dirección y sentido. Por tanto, la suma mencionada debe ser una suma vectorial. Esto quiere decir que el resultado final depende del ángulo formado por las direcciones de la sonda y del planeta, y de si la sonda se mueve "a favor" del planeta o "en contra". Concretamente, el valor absoluto de la velocidad sería (V²+U²+2VUcosθ)^1/2, siendo θ el ángulo formado por ambas direcciones. Para simplificar un poco, imaginemos que la sonda se mueve en la misma dirección que el planeta, pero en sentido contrario. Su velocidad sería V-U.

Sigamos. Tras rodear el planeta y alejarse, al alcanzar de nueva una distancia D con respecto al mismo, la sonda tiene una velocidad V con respecto a él. Pero tiene una velocidad V+U (suma vectorial) con respecto a nosotros. Si volvemos al ejemplo simplificado, y suponemos que tras la maniobra, las velocidades de la sonda y el planeta tienen la misma dirección y sentido, la velocidad con respecto a nosotros sería de V+U (suma escalar). Es decir, en este ejemplo simplificado, habremos aumentado la velocidad con respecto a nuestro sistema de referencia (el Sol, recordemos), en 2 veces la velocidad del planeta.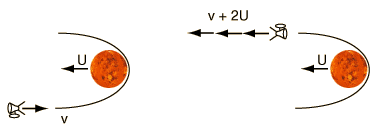

En realidad, este caso simplificado, en el que el acercamiento y alejamiento son paralelos al movimiento del planeta, nunca sucedería, ya que estas trayectorias tienen formas parabólicas o hiperbólicas, pero ilustra de forma sencilla lo que ocurre: la velocidad final de la sonda es diferente.

¿Y de dónde sale la energía? La sonda ha aumentado su energía cinética tras el encuentro con el planeta. ¿No viola eso el principio de conservación de la energía? No, pues esa energía extra la ha obtenido de la energía cinética del planeta. Recordemos una vez más otro principio fundamental de la mecánica clásica: la conservación de la cantidad de movimiento. La cantidad de movimiento de un cuerpo es el producto entre su masa y su velocidad. La cantidad de movimiento total de un sistema cerrado debe conservarse, es decir, la suma de las cantidades de movimiento de cada objeto debe mantenerse. Es decir: m·V₁+M·U₁=m·V₂+M·U₂, donde m es la masa de la sonda, M la del planeta, V₁ la velocidad inicial de la sonda, V₂ la velocidad final de la misma, U₁ la velocidad inicial del planeta, y U₂ su velocidad final.

Entonces ¿modificamos la órbita de un planeta cada vez que una sonda lo utiliza como honda gravitatoria? Pues sí, pero hay que tener en cuenta la inmensa diferencia entre las masas de la sonda y el planeta. Si en la ecuación anterior despejamos la velocidad final de éste (U₂), nos quedaría U₂=U₁+(V₁-V₂)·m/M. Si M es muy grande con respecto a m, como ocurre en realidad (la masa de la Tierra, por ejemplo, es de casi 6×10²⁴ kg, es decir, un 6 seguido de 24 ceros), la variación de velocidad del planeta es prácticamente nula.

Una vez comprendido el funcionamiento de una honda gravitatoria, nos daremos cuenta de varias cosas: por un lado, el incremento de la velocidad depende de los ángulos que forman las trayectorias inicial y final de la sonda, con respecto al movimiento del planeta. La velocidad de la sonda puede incrementarse o disminuir, dependiendo de estos ángulos. Volviendo a un ejemplo simplificado, si la sonda se acerca al planeta por detrás, y gira 180º, habrá disminuido su velocidad en 2 veces la del planeta.

Por otro lado, la variación de velocidad de la sonda depende de la velocidad del cuerpo utilizado. Esto quiere decir que no podemos utilizar el Sol como honda gravitatoria dentro de nuestro sistema solar. Sólo serviría para modificar el rumbo, pero no conseguiríamos incrementar la velocidad. Podría tener utilidad a la hora de dirigir la sonda hacia otro sistema estelar, cuya estrella (o estrellas) se muevan con respecto a nuestro Sol, pero no para dirigirla hacia Saturno, por ejemplo.

Así que lo que realmente produce estos cambios de velocidad (y por tanto, ahorro de combustible, que es el motivo fundamental de todo esto), es el movimiento del planeta en cuestión. El nombre honda gravitatoria o asistencia gravitatoria puede llevar a confusión, y hacer pensar a más de uno que simplemente se necesita un cuerpo más o menos masivo, cuando en realidad se necesita un cuerpo más o menos masivo, en movimiento.

¿Y si se utilizan los propulsores durante la maniobra? Bueno, eso es otro tipo de maniobra, de la que hablaré mañana.